فيثاغورس هو اسم العالم الذي اخترع النظرية، ونُسب اسمها إلى اسمه، وقد كان من أكفأ المؤهلين من الناحية العلمية، حيث اهتم بعلم الهندسة والكونيات في شبابه، وهو ما ساعده على التفوق في الرياضيات، ومن ثمّ وضع نظرية فيثاغورس الشهيرة.
عناصر البحث

- مقدمة البحث.
- نص قانون فيثاغورس.
- إثبات نظرية فيثاغورس.
- تطبيقات نظرية فيثاغورس.
- خاتمة البحث.
تحميل بحث عن نظرية فيثاغورس PDF
مقدمة بحث عن نظرية فيثاغورس
فيثاغورس هو عالم يوناني متخصص في الرياضيات منذ ما يسبق قبل الميلاد، وقد وضع نظرية فيثاغورس التي عُدت واحدة من أقدم النظريات الرياضية المعروفة منذ قديم الزمان، والتي بفضلها تم تسهيل أداء العديد من المهام في مجالات مختلفة.
نص قانون نظرية فيثاغورس
تنص نظرية فيثاغورس على أن مجموع مربعيّ طوليّ ضلعيّ الزاوية القائمة (الضلعين الأقصر في المثلث) مساوٍ لمربع طول الوتر (الضلع الأطول في المثلث)، أما عن النظرية بالرموز: نظريّة فيثاغورس= أ²+ ب²=ج².
حيث (أ، ب) هما ضلعا المثلث القائم، و(ج) هو وتر المثلث القائمة، مع العلم أن معكوس النظرية أيضًا صحيح؛ لأن أي مثلث تنطبق عليه النظرية هو مثلث قائم الزاوية.
لا يفوتك أيضًا: بحث عن الذكاء الاصطناعي مختصر بالمراجع PDF
إثبات نظرية فيثاغورس
يُمكن استخدام عدد كبير جدًا من البراهين لإثبات نظرية فيثاغورس، وهو ما نشره عالم الرياضيات “إليشا سكوت لوميس” في كتابه “فرضية فيثاغورس” الذي تم إطلاقه عام 1927م، حيث قدّم أكثر من 370 برهان مختلف للنظرية، تم تقسيمها إلى أربعة أقسام.
- قسم الهندسة (المساحات).
- قسم الجبر (جوانب المثلث).
- قسم الديناميكية/ الحركية (خصائص القوة والكتلة).
- قسم المتجهات.
شاع الإثبات الهندسي لنظرية فيثاغورس بين عدد كبير من الناس على مر السنوات، وهو ما يتم وفق الخطوات التالية:
- نفترض أن هناك مربع نقاطه (د، هـ، و، ي) على أضلاعه الأربعة، بحيث تقسم كل نقطة منها الضلع إلى قسمين.
- نعتبر طول الضلع الأول (أ)، وطول الضلع الثاني (ب)، ثم نوصل النقاط ببعضها بخطوط مستقيمة لتكوين مربع داخلي طول ضلعه (ج)، إضافةً إلى أربع مثلثات داخلية قائمة الزاوية وترها هو الضلع (ج)، وطول ضلعيها الآخرين (أ، ب).
- ينتج أن طول ضلع المربع الخارجي (أ +ب)، لذا فإن مساحة المربع الخارجي تساوي (أ +ب) ²، وهي نفسها مساحة المثلثات الأربعة.
- مساحة المثلثات الأربعة = 4* (1/2 طول القاعدة* الارتفاع) = 2/4 *أ *ب = 2 أ ب، بينما مساحة المربع الداخلي = جـ²
- نتوجه لإيجاد مساحة المربع الخارجي، وهي: (أ+ب) ²= 2أب+ ج²، ثم فك التربيع لتبسيط الصورة، حتى تصبح أ²+2أب +ب²= 2أب+ ج².
- ترتيب طرفيّ المعادلة حتى تصبح على الشكل: أ²+ب²= 2أب+ ج²-2أب.
- اختصار الحدود لتصبح المعادلة على النحو: أ² + ب² = ج²، وهو ما يثبت النظرية، حيث إن (ج) هو الوتر، فينتج أن مربع الوتر يساوي مجموع مربعيّ الضلعين.
لا يفوتك أيضًا: بحث عن الحاسب الآلي وأنواعه جاهز للتحميل PDF
تطبيقات نظرية فيثاغورس
1- حساب جهات المثلثات
فيثاغورس هي النظرية التي توضح أطوال جهات المثلث قائم الزوجة، وهي الطريقة المستخدمة بشكل شائع حتى وقتنا هذا في حل المسائل الرياضية المتعلقة به.
2- تحديد زوايا المربع
إنّ التأكد من الشكل المربع سواء في المسائل الرياضية، أو شكل المباني على أرض الواقع هي مهمة تتم من خلال نظرية فيثاغورس، حيث تُطبق على المثلث الذي أطوال أضلاعه 3، 4، 5 سنتيمترات.
حيث إنها القياسات الخاصة بالمثلث قائم الزاوية، أي أن إحدى زواياه قياسها 90 درجة، وهو ما يساعد البناؤون عند رغبتهم في بناء زاوية بين جدارين، بحيث يقوموا بتشكيل مثلث من ثلاثة حبال طولها مساوٍ للأطوال السابقة.
فتكون الزاوية الواقعة بالجهة المعاكسة هي وتر المثلث، وهي الزاوية القائمة، والتي يُمكن من خلالها التأكد من صحة وضعية الجدران، أو الأساس بالخطوط الصحيحة.
3- فيثاغورس في البناء
أحيانًا يستخدم البناؤون نظرية فيثاغورس لحساب طول القطر الواصل بين خطين مستقيمين، خاصةً في مشاريع الأبنية المادية، أو الأعمال الخشبية، مثل بناء السطح المائل.
4- المسافة بين نقطتين
تستخدم نظرية فيثاغورس أيضًا في حساب مسافة الخط المستقيم الواصل بين نقطتين على مستوى السينات والصادات، وهي الإحداثيات الافتراضية لأي نقطتين (س، ص).
5- فيثاغورس في الملاحة
حيث تستخدم النظرية في حساب أقصر مسافة يُمكن أن تكون بين نقطتين في النظام ثنائي الأبعاد، وهو ما يفيد مثلًا شخص على متن سفينة في البحر، ويرغب في الوصول إلى نقطة بعيدة عن الجهة الشمالية بمقدار 300 ميل، والجهة الغربية بمقدار 400 ميل..
باستخدام قانون فيثاغورس يتمكن من معرفة المسافة بينه وبين تلك النقطة، إضافةً إلى حساب درجات الزاوية التي يلزم معرفتها للوصول إليها.
يتم ذلك من خلال افتراض المسافات للغرب والشمال هي جهات المثلث، وأن أقصر مسافة للوصول هي قطر المثلث، ثمّ التعويض بالرموز والأرقام وحل المعادلة.
هناك البعض ممن يستخدمون هذا القانون في الملاحة الجوية أيضًا، من خلال استخدام ارتفاع الطائرة عن سطح الأرض، والمسافة بينها وبين جهة الوصول الواقعة في المطار.
6- فيثاغورس في وسائل النقل
إنّ إيجاد الجهة الأطول من المثلث قائم الزاوية هو أمرٌ هام جدًا في هبوط الطائرات، حيث يتم حساب الدرجة التي ستهبط عندها الطائرة.
أما في مجال النقل البري فإن النظرية تُسهم في حساب قيمة الوتر وتحديد كمية الحبال اللازمة لنقل المنقولات في الشاحنات من نقطة لأخرى، وهو ما يضمن الحفاظ على الأرواح والمنقولات من الانهيار، خاصةً إن كان حجمها ضخم.
7- فيثاغورس في مسح الأراضي
مسح الأراضي هي المهمة التي تُطلق على ما يقوم به رسامو الخرائط لحساب المسافات والارتفاعات الرقمية بين النقاط المختلفة قبل رسم الخريطة، ونظرًا لأنه غالبًا ما تكون التضاريس غير متساوية؛ يلجأ الرسامون إلى الطرق التي تجعل قياسات المسافات تسير بنظام معين.
8- فيثاغورس في علم الفلك
تُسهم فيثاغورس في معرفة المسافات بين الكواكب والنجوم، وهو ما يُشكل أهمية كبيرة في علم الأفلاك، لكن لا يُستخدم القانون بشكل مباشر، وإنما تُستخدم نسخة معدلة منه، وهي: ج^2= أ^2 + ب ^2 – 2*أ*ب*جتا ج
يرجع استخدام هذه المعادلة إلى الحقيقة التي تثبت أن ليست جميع الزوايا في الفضاء قوائم؛ بسبب المدارات غير الدائرية، وصعوبة ضبط المسافة الأصلية أو حسابها.
أما في حال كانت الزاوية قائمة، يُستخدم القانون الأصلي، وهو: ج^2= أ^2 + ب ^2؛ لأن قيمة جتا الزاوية القائمة تساوي صفر، وهو ما يساوي الجزء الأخير في المعادلة الذي يأتي بعد الإشارة السالبة بصفر.
لا يفوتك أيضًا: بحث عن الرياضيات في حياتنا كامل PDF
خاتمة بحث عن نظرية فيثاغورس
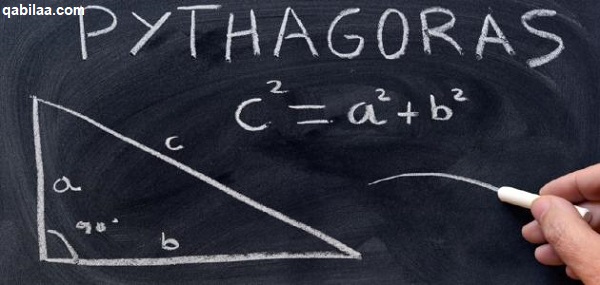
كان للأرقام أهمية ومعاني كبيرة لدى علماء العصور الماضية مقارنةً بعلماء الوقت الحالي، حتى أن العالم فيثاغورس كان يرى أن كل شيء في الكون حوله عبارة عن أرقام، وقد عُدت فيثاغورس النظرية الأشهر في العالم قبل آلاف السنين.
ظهرت نظرية فيثاغورس في بادئ الأمر بشكل معقد للغاية، حتى أتى العالم فيثاغورس وتمكن من إثبات صحتها بطريقة مُبسطة سهلت استخدامها في مجالات عديدة، ومنذ هذا الوقت نُسبت إليه.